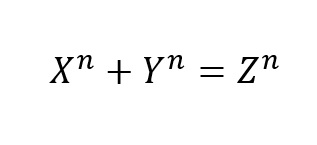By: Pierre-Selim
サイモン・シンの『フェルマーの最終定理』を読み終えたので、その感想を書いていきます。
ボク自身、数学の世界にはあまり興味がない人間ですが、フェルマーの最終定理は聞くところによると、300年もの間天才数学者達に狂気と苦痛を与えた大問題らしいので、これを機に勉強しました。
フェルマーの最終定理とは？
フェルマーの最終定理とは、17世紀前半に活躍した「ピエール・ド・フェルマー」と言うアマチュアの数学者が残した定理のことです。
内容的には中学生でも理解できるものですが、300年以上もの間、数々の天才数学者を苦しめる悪魔的難問の１つです。
フェルマー自身は数学に関しては天才的な頭脳を持っており、数々の斬新な定理や証明方法を見つけ出しますが、名誉心が乏しいせいか、後世に自分の実績を残すために本を出版したりノートに記録するのを全くしなかったそうです。
彼の死後、彼の息子さんがフェルマーの残した数学のメモとかを寄せ集めて、1冊の本を出します。
どの定理の証明や問題も難問ばかりでしたが、数学者達の努力もあって、次々と証明をしていき、残すところ、あと1問まで来ました。
しかし、最後の1問が歴史に名を残す悪魔的難問だったのです。
ｎ≧３の時、この式を満たすｘ、ｙ、ｚの値は存在しない。
私はこの命題の真に驚くべき証明をもっているが、余白が狭すぎるのでここに記すことはできない。
つまり、この問題の意味は以下の通りです。
フェルマーの最終定理の意味を分かりやすく解説するよ
ｎ＝１の時、上の式は「Ｘ＋Ｙ＝Ｚ」となるわけですが、この式が成り立つｘ、ｙ、ｚの組み合わせは無数にあります。
ｎ＝２の時には、「Ｘ²＋Ｙ²＝Ｚ²」と言う式になりますが、これは「ｘ＝３、ｙ＝４、ｚ＝５」などと、いくつもの解があります。
しかし、ｎ＝３以上になった時に、上の式を満たすｘ、ｙ、ｚの組み合わせが全くなくなると言う不思議。
これを数学的に証明しろ、と言うのがフェルマーの最終定理なのです。
ちなみに、ｎ＝３以上は成り立たないのを証明する、と言うのは、３～1億までのｎを証明すれば良いと言う物ではありません。
100億まででも１兆まででもダメで、無限に続くｎの場合を全て証明しないといけない、と言うのがこの問題の難しいところなのです。
本書は数学者達の熱い人間ドラマ
本書では、多少は数学的な知識が書かれていますが、簡潔に書かれているし、数学的な内容よりもフェルマーの最終定理に携わった数学者達の数学に対する熱い思い、苦悩、夢などに焦点が当てられています。
例えば、フェルマーの最終定理に挑戦することにした数学者、アンドリュー・ワイルズは、フェルマーの最終定理への思いが強すぎて、数学界では常識外の行動に出ています。
ワイルズ教授が単独でフェルマーの最終定理の完全な証明に成功したとなると、数学界最高の名誉は彼一人のものになるだろう。その一方で、ワイルズは秘密主義をとったツケを払わなければならなかった。
それは、前もって自分のアイディアを数学者仲間と議論したり検証したりできなかったということ、そしてそれゆえに、彼の証明が根本的なところで誤っている可能性は決して小さくないということだ。
「フェルマーの最終定理」p.34
普段、ボクたちは仕事をやる上では、上司や同僚に相談したりアドバイスを受けることで、自分は今どんな仕事をすれば良いかの判断材料にしたり、新たな仕事のやり方を見つけたりできます。
数学界でも同じで、仲間とアイディアを出し合うことでモチベーションを高めたり、今まで知らなかった手法やアイディアを手に入れることができるようです。
しかし、ワイルズは上記のメリットを排除してまでも、子供の頃からの夢だった「フェルマーの最終定理を証明した」たった１人の人物になりたかったのです。
ここまで人を動かすものは、おそらくフェルマーの最終定理ぐらいかもしれません。
[amazonjs asin=”4102159711″ locale=”JP” title=”フェルマーの最終定理 (新潮文庫)”]
