数学と統計学の大きな違いは、統計学がデータの収集、記述、分析、解釈、表現に関する学問であるのに対し、数学は数、量、空間に関する抽象的な学問であることである。
統計学も数学も数字や桁を扱うが、両分野にはかなりの違いがあります。
統計学とは
統計学は応用数学の一分野であり、データの収集、記述、分析、解釈に関する学問です。
統計学は、科学分野や研究の文脈で多用されている。
統計学では、より小さなグループの特徴や観察可能な行動を考慮するだけで、より大きなグループでの結論が導き出されます。
このように、これらのサンプルはより大きなグループの一部を表しています。
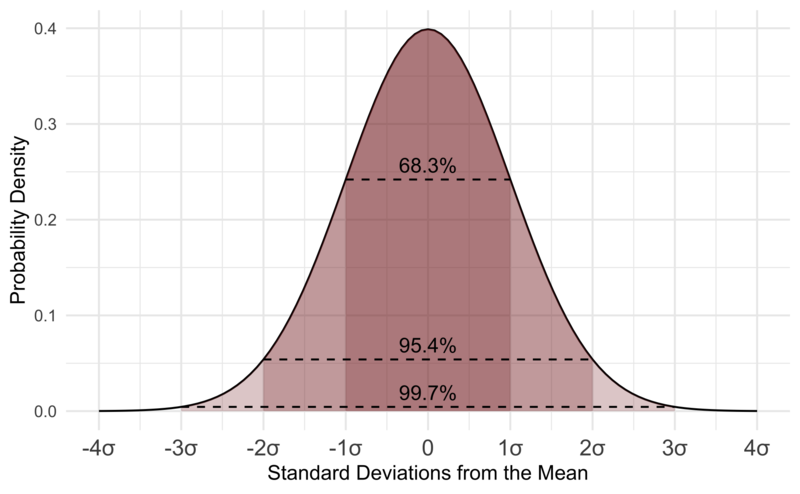
統計学には2つの大きな分野があります。
それは記述統計と推測統計です。
記述統計はサンプルと母集団のデータの特性を記述し、推測統計はこれらの特性を用いて仮説を検証し、結論を導き出すものです。
記述統計は、変数の平均値、標準偏差、頻度など、サンプルやデータセットの特性を記述したり要約したりする。
一方、推測統計は、データセット内の変数を互いに関連付けるために、例えば、相関分析や回帰分析など、様々な手法を用いる。
例えば、相関分析や回帰分析などを用いて、データ中の変数を互いに関連付ける。
これにより、予測や因果関係を推測することができる。
同時に、記述法、平均法、分散法、推論法、線形回帰分析などの統計ツールもあります。
さらに、統計学は、社会科学、ビジネス、人文科学、政府、製造業などで有用です。
統計学の分野では、不確実性と変動という2つの基本的な考え方があります。
数学とは何か
数学は数、量、空間に関する科学であり、数を数える、測る、形や動きを系統的に研究するといった基本的な実践から発展したものです。
数学者はパターンを探し、新しい推測を立て、真理を確立する。
数学は、論理的推論と数量的計算の組み合わせと表現することができる。
数学は、自然科学、工学、医学、社会科学など、多くの重要な分野で不可欠なツールとなっています。
また、応用数学は、数学的知識の他分野への応用や新しい数学的発見に関する数学の一分野です。
数学的活動の多くは、純粋な推論によって抽象的な対象の性質を発見し、証明することにある。
数学には、算術、幾何学、整数論、代数学、離散数学など、多くの分野があります。
数論は自然数を扱い、幾何学は直線、角度、円などの図形を扱う。
一方、代数学は方程式や公式の立式に重点を置く。
全体として、これらの数学のすべての枝は、私たちの日常生活の中で役立つことができます。
統計学と数学の共通点
- 統計学も数学も、様々な分野で役立っています。
- 統計学と数学は数字や桁を使う。
統計学と数学の違い
定義
統計学はデータの収集、記述、分析、解釈に関する学問であり、数学は数、式、関連構造、図形とそれらが含まれる空間、量とその変化などのテーマを含む抽象的な科学です。
サブカテゴリー
統計学には記述統計学と推測統計学があり、数学には算術、幾何学、代数学、整数論などの下位カテゴリがあります。
用途
統計学はビジネス、人文科学、行政、製造業などの分野で利用されているが、数学は自然科学、工学、医学、社会科学など多くの分野で利用されている。
代表的なもの
統計学では、小集団の観察行動を考慮して大集団の結論を出すが、数学では、小集団の行動を考慮して結論を出すことはない。
結論
数学は空間の理解、尺度、質の研究を中心とする抽象科学であるのに対し、統計学はデータの収集、分類、表現に焦点を当てた応用科学の一分野です。
したがって、これが数学と統計学の大きな違いです。
