線形計画法と非線形計画法の主な違いは、線形計画法は線形関係を持つ一連のパラメータや要件から最適な解を求めるのに役立ち、非線形計画法は非線形関係を持つ一連のパラメータや要件から最適な解を求めるのに役立つという点です。
線形計画法は、与えられた問題に対して最も最適な解を求めることができるため、数学の最適化手法において重要な概念です。
一方、非線形計画法は、非線形である制約条件や目的関数を考慮して最適な解を求める数学的手法です。
線形計画法とは
線形計画法とは，与えられたパラメータまたは要件のセットから，可能な限り最良の結果または解決策を決定することができる数学的方法である．これらのパラメータや要件は線形関係にある。
さらに、線形計画法の主な利点は、利用可能な資金、エネルギー、資源、時間、空間、その他の関連する要因や変数に応じて、最適なソリューションを見つけるためのモデリングやシミュレーションの実行を支援することです。
さらに、線形計画法の成果は、利益の最大化とコストの削減です。
図1：線形計画法のグラフ例
線形計画法の基本的な構成要素は以下の通りです。
決定変数 – 決定する量
目的関数 – 各決定変数が最適化すべき性質にどのような影響を与えるかを表す
制約条件 – 各決定変数が限られた量の資源をどのように使用するかを表現します。
データ – 目的関数と制約条件の関係を説明します。
非線形計画法とは
非線形計画法とは，非線形制約や非線形目的関数に関係する最適化問題を解くことです．非線形目的関数を束縛制約，線形制約，非線形制約などの条件下で最小化または最大化することが含まれます．これらの制約には不等式と等式があります。
また、非線形計画法は、計算金融における設計トレードオフの分析、最適設計の選択、最適軌道の計算、ポートフォリオの最適化、モデルのキャリブレーションに役立つ。
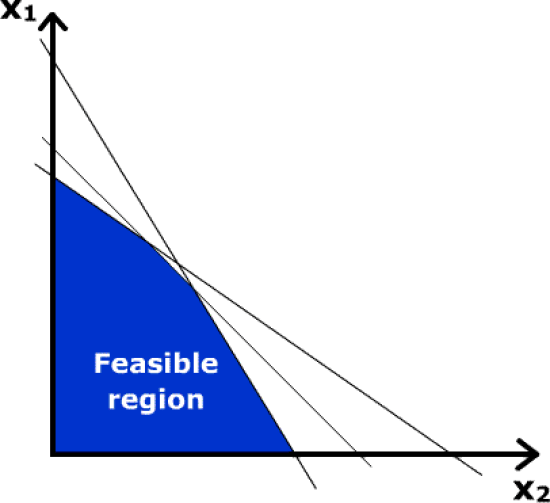図2：非線形計画法のグラフ例
非線形計画法には、以下の2種類があります。
無制限非線形計画法
制約なし非線形計画法では、非線形スカラー関数f(x)の局所最小となるベクトルxを求めます。
準ニュートン、ネルダーミード、トラストリージョンなどが一般的な制約なし非線形計画法のアルゴリズムです。
制約条件付き非線形計画法
制約付き非線形計画法では、1つ以上の制約条件下で非線形関数f(x)を最小化するベクトルxを求めます。
内点法、逐次二次計画法、信頼領域法などは、一般的な制約付き非線形計画法のアルゴリズムです。
Linear Programming と Nonlinear Programming の違い
定義
線形計画法は、要件が線形関係で表される数理モデルにおいて最良の結果を得るための方法であるのに対し、非線形計画法は、制約条件や目的関数が非線形である最適化問題を解くプロセスです。
このように、線形計画法と非線形計画法の主な違いはここにあります。
使用方法
また、線形計画法は線形である制約条件を用いて問題の最適解を求めるものであり、非線形計画法は非線形である制約条件を用いて問題の最適解を求めるものです。
結論
線形計画法と非線形計画法の主な違いは、線形計画法は線形関係を持つ一連のパラメータや要件から最適解を求めるのに役立ち、非線形計画法は非線形関係を持つ一連のパラメータや要件から最適解を求めるのに役立つという点です。
