プリムスアルゴリズムとクルーシャルアルゴリズムの主な違いは、プリムスアルゴリズムがルート頂点から始まる最小スパニングツリーを生成するのに対し、クルーシャルアルゴリズムは最小加重エッジから始まる最小スパニングツリーを生成する点です。
アルゴリズムとは、ある問題を解決するために従うべき一連の手順です。
貪欲アルゴリズムでは、与えられた解の領域から判断を行うことができる。
局所的な最適解を発見し、全体最適解を見つけることにつながることがあります。
PrimのアルゴリズムとKrushalのアルゴリズムは、2つの貪欲アルゴリズムです。
最小分散木は、すべての分散木の中でコストが最小となる分散木です。
主にネットワーク設計に利用される。
この2つのアルゴリズムにより、最小分散木を求めることができる。
プリムスアルゴリズムとは?
プリムスアルゴリズムは、グラフから最小木(Minimum Spanning Tree)を求めるためのアルゴリズムです。
グラフのすべての頂点を含む辺の部分集合を決定する。
また、エッジの重みの和を減らすこともできる。
また、このアルゴリズムは、ルートノードから始まり、各ステップですべての接続エッジを含むすべての隣接ノードをチェックする。
さらに、サイクルを発生させない重みの少ないエッジを選択する。
本アルゴリズムの手順は以下の通りです。
ステップ1 – 開始頂点またはルート頂点を選択する。
ステップ2 – フリンジ頂点ができるまで、ステップ3と4を繰り返す。
ステップ3 – 木の頂点とフリンジ頂点を結ぶ辺のうち、重みが最小のものを選択する。
ステップ4 – 選択した辺と頂点を最小木に追加します。
Krushalアルゴリズムとは?
Krushal’s Algorithm は、連結された重みつきグラフの最小木 (minimum spanning tree) を求めるためのアルゴリズムです。
これは、グラフのすべての頂点を横切ることができる辺の部分集合を求めるものです。
このアルゴリズムは、全体最適を求めるのではなく、各段階での最適解を求める。
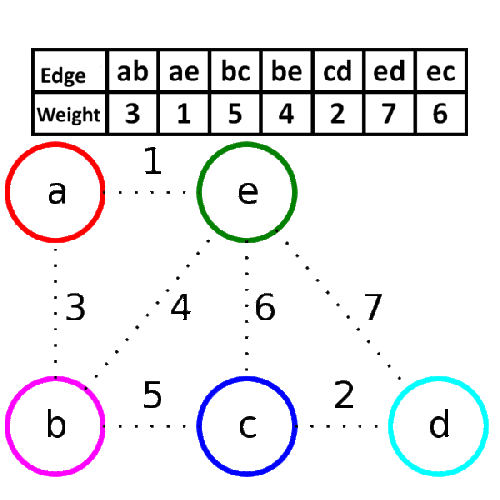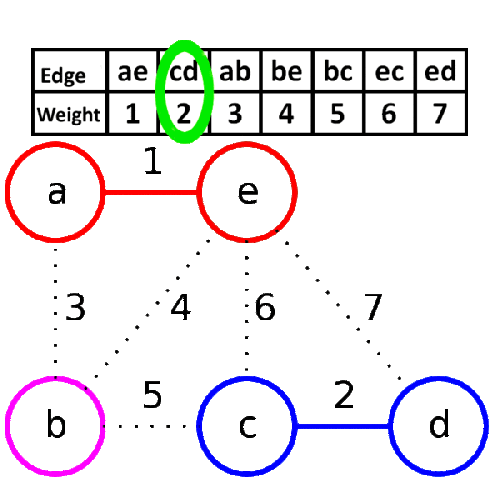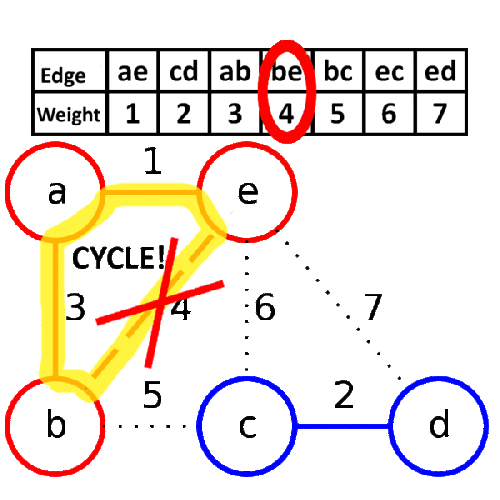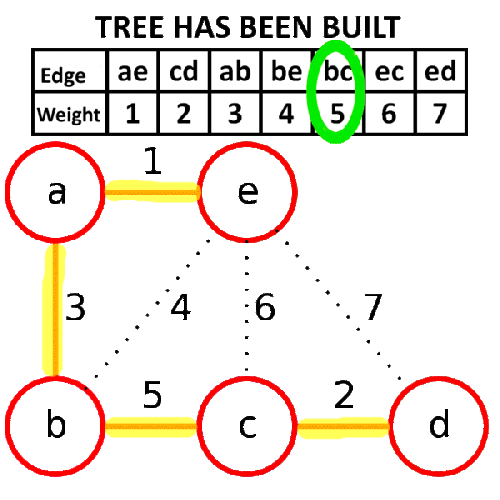
アルゴリズムの手順は以下の通りです。
ステップ1- forestを作成する。
forestの各グラフは独立した木です。
forest は離散化されたトレスの集まりです。
ルートノードと、ルートノードと第1レベルノードを結ぶエッジを削除することで得ることができる。
Step 2- グラフのすべてのエッジからなる優先キューを作成する。
手順3-優先度待ち行列が空でなければ、手順4と5を繰り返す。
手順4-優先度待ち行列からエッジを削除する。
ステップ5-ステップ4の結果のエッジが2本の木をつないでいれば、それをforestに追加し、そうでなければエッジを破棄する。
プリムスとクルシャールアルゴリズムの違い
定義
プリムのアルゴリズムは、重み付き無向グラフの最小生成木を求める貪欲なアルゴリズムであり、クルーシャルのアルゴリズムは、森の中の任意の2つの木を結ぶ最小重量の辺を求める最小生成木アルゴリズムです。
これがプリムスとクルーシャルアルゴリズムの主な違いです。
世代
また、Primのアルゴリズムでは、ルート頂点から始まる最小木が生成される。
しかし、Krushalのアルゴリズムでは、最小の重みのエッジから最小の木を生成する。
選択
プリムアルゴリズムとクルシャルアルゴリズムのもう一つの違いは、プリムアルゴリズムがルート頂点を選択するのに対し、クルシャルアルゴリズムは最短辺を選択する点です。
手順
プリムのアルゴリズムがルート頂点に接続する最短辺を選択するのに対して、クルーシャルのアルゴリズムはその次の最短辺を選択する。
ここもプリムとクルシャルのアルゴリズムの違いです。
結論
プリムスアルゴリズムとクルーシャルアルゴリズムは、グラフから最小木(minimum spanning tree)を求めるのに役立つ。
プリムアルゴリズムとクルーシャルアルゴリズムの違いは、プリムアルゴリズムがルート頂点から始まる最小生成木を生成するのに対し、クルーシャルアルゴリズムは最も重みのない辺から始まる最小生成木を生成する点です。
