BFSとDFSの主な違いは、BFS（Breadth First Search）がレベルごとに進むのに対し、DFS（Depth First Search）は開始ノードから終了ノードまでの経路をたどり、その後、開始ノードから終了ノードまでの別の経路に移り、全ノードを訪問するまで続ける点です。
グラフは、データ要素をネットワークモデルとして配置した非線形データ構造です。
グラフのノードは頂点と呼ばれ、これらのノードを結ぶのがエッジです。
ほとんどのグラフ問題は探索手法で解くことが可能である。
一般的に使われている探索手法として、BFS（Breadth First Search）とDFS（Depth First Search）があります。
簡単に説明すると、BFSは待ち行列を、DFSはスタックを使用する。
BFSとは
BFSとは、Breath First Searchの略で、ブレスファーストサーチのことです。
待ち行列を利用します。
処理の流れは以下の通りです。
- 開始頂点を訪問し、その要素を待ち行列に入れる。
- 隣接する未訪問の頂点への訪問を繰り返し、キューから頂点を削除する。
- 新たに訪れた頂点を待ち行列に入れる。
以下はその例です。
上図の開始頂点を 1 とすると、1 に接続するノードは 2 と 4 です。
そこで、1, 2, 4 を待ち行列に入れることができる。
出力は1,2,4です。
1 については、残りの頂点がない。
したがって、1を待ち行列から取り除くことができる。
次に、2に移る。
2の隣接頂点は、3, 5, 6です。
従って、3,5,6 を待ち行列に入れることができる。
出力は、1, 2, 4, 3, 6です。
この3つの数字に加えて、2に接続する隣接頂点がないので、2を待ち行列から外すことができる。
4に隣接するノードは6のみであり、すでに訪問済みです。
4にはもう頂点がない。
よって、4を待ち行列から取り除くことができます。
この作業を、キューが空になるまで繰り返さなければならない。
これは探索操作の終了を意味する。
DFSとは
DFSとは、Depth First Searchの略です。
処理の流れは以下の通りです。
隣接する未訪問の頂点を訪問し、訪問済みとしてマークする。
そして、それを出力に表示し、スタックに格納する。
隣接する頂点が見つからなければ、スタックから頂点をポップアップする。
上記 2 つのステップを、スタックが空になるまで続ける。
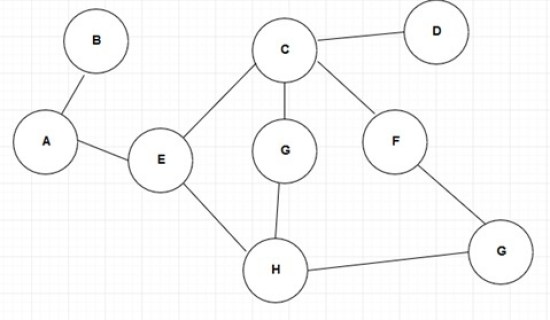図 2: DFS
開始頂点は A であり，スタックに押し込まれている．隣接する頂点は B と E です。
B をスタックに押し込むことができる。
B に隣接するノードはないので，B をスタックから取り出すことができる．A に隣接する残りのノードは E なので、E をスタックにポップすることができる。
これで、出力は A B E となります。
A に隣接するノードがないので，A をスタックから取り出すことができる．E の隣接ノードは C と H です。
ここで C を考える。
出力は A B E C です。
この処理は、スタックが空になるまで続けられる。
これは探索操作を終了させる。
BFSとDFSの違い
定義
BFS (Breadth first search) は、グラフのルートノードからグラフを走査し始め、隣接するすべてのノードを探索するグラフ走査アルゴリズムです。
DFS (Depth first search) は、グラフの最初のノードから始めて、必要なノードまたは子ノードを見つけるまでどんどん深く探索するアルゴリズムである。
これがBFSとDFSの主な違いです。
長文
BFSがBreadth First Searchの略であるのに対して、DFSはDepth First Searchの略です。
ノードの格納方法
BFSとDFSのもう一つの大きな違いは、BFSがキューを使うのに対して、DFSはスタックを使うことです。
メモリ消費量
さらに、BFSはDFSよりもメモリを多く消費する。
トラバースの方法
BFSとDFSのもう一つの違いは、探索の方法です。
BFSは最も古く未訪問の頂点から順に訪問することを重視し、DFSはエッジに沿った頂点を最初に訪問することを重視する。
結論
BFSとDFSは、グラフの中のある要素を見つけるための探索手法です。
BFSとDFSの主な違いは、BFSはレベルごとに進むのに対し、DFSは開始ノードから終了ノードまでの経路をたどり、その後、開始ノードから終了ノードまでの別の経路に移り、すべてのノードを訪問するまで続ける点です。
