有向グラフと無向グラフの主な違いは、有向グラフが頂点の順序付きペアを含むのに対し、無向グラフは頂点の順序なしペアを含むことである。
グラフは、リンクで結ばれたオブジェクトの集合を絵にしたような非線形データ構造です。
グラフはデータをネットワークとして表現する。
グラフの主要な構成要素は、頂点とエッジの2つです。
頂点はデータ要素であり、エッジは頂点同士をつなぐリンクです。
グラフには、主に有向グラフと無向グラフの2種類があります。
有向グラフとは
グラフの頂点の組が順番に並んでいるものを有向グラフという。
グラフの辺は、ある頂点から別の頂点への特定の方向を表す。
(V1, V2)という辺の表現があるとき、その方向はV1からV2までです。
最初の要素V1が初期ノードまたは開始頂点です。
2番目の要素V2は終端ノードまたは終端頂点です。
上のグラフで、頂点Aは頂点Bに接続する。
Aは初期ノード、Bは終点ノードです。
したがって、BからAへの方向は考慮できない。
同様に、頂点 D は頂点 B に接続する。
D は初期ノードで、B は終端ノードです。
同様に、接続された頂点は特定の方向を持つ。
頂点の集合(V) – {A, B, C, D, E, F}。
辺の集合(E) – {(A,B),(B,C),(C,E),(E,D),(D,E),(E,F)}.
無向グラフとは
When a graph has an unordered pair of vertexes, it is an undirected graph. In other words, there is no specific direction to represent the edges. The vertexes connect together by undirected arcs, which are edges without arrows. If there is an edge between vertex A and vertex B, it is possible to traverse from B to A, or A to B as there is no specific direction.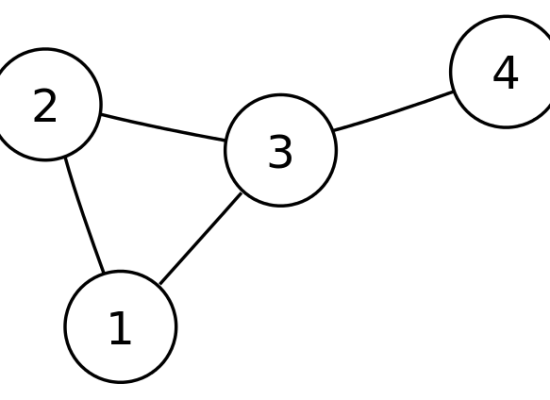
上のグラフは無向グラフです。
どの辺にも方向がない。
2から3、3から2、1から3、3から1などへたどることができる。
頂点の集合(V) – {1, 2, 3, 4}。
辺の集合(E) – {(1, 2), (2, 1), (2, 3), (3, 2), (1, 3), (3, 1), (3, 4), (4, 3) }。
有向グラフと無向グラフの違い
定義
有向グラフは頂点の順序対を含むグラフであり、無向グラフは頂点の無順序対を含むグラフです。
これが有向グラフと無向グラフの大きな違いです。
方向性
さらに、有向グラフでは、辺は頂点の方向を表す。
しかし、無向グラフでは、辺は頂点の向きを表さない。
この点も、有向グラフと無向グラフの違いと言える。
代表的なもの
また、有向グラフと無向グラフの大きな違いは、表現記号です。
有向グラフでは矢印が辺を表し、無向グラフでは無向の円弧が辺を表す。
結論
グラフには有向グラフと無向グラフの2種類があります。
有向グラフと無向グラフの主な違いは、有向グラフは順序のある頂点の組を含むのに対し、無向グラフは順序のない頂点の組を含むことである。
