主な違い – 六角形と単斜格子の単位胞
六角形と単斜晶系単位胞という言葉は、結晶系に関係する言葉です。
結晶系とは、立方晶、正方晶、斜方晶、三角晶、六方晶、単斜晶、三斜晶の7種類の結晶を、結晶軸の関係によって分類したものです。
結晶系の単位胞は、結晶系の繰り返しパターンを表す構造の一部分です。
代表的な原子と、その原子の繰り返し配列からなる。
単位胞は3次元構造であり、結晶系はそれぞれ固有の単位胞構造を持っています。
単位胞は箱です。
原子が異なるユニークなパターンで配置されたものです。
この単位胞は、単位胞の辺と角の間の長さである格子定数に関して記述される。
六角形と単斜体の主な違いは、六角形の単位セルの3つの軸のうち2つは同じ長さであるのに対し、単斜体の単位セルは3つの軸が不等長であることである。
ユニットセルとは
単位胞とは、結晶系の繰り返しパターンを表す小さな構造です。
箱型構造です。
この箱には、材料に存在するすべての種類の原子が含まれています。
3次元構造です。
単位セルは、格子パラメータを使用して記述されます。
格子とは、金属などの結晶性固体における原子、イオン、分子の規則的な繰り返しの3次元配列のことです。
格子定数は、単位格子の辺と角の間の長さです。
長さ（軸ともいう）はa、b、cの記号で与えられ、角度はα（アルファ）、β（ベータ）、γ（ガンマ）の記号で与えられる。
セル内の原子の位置は、X、Y、Zで与えられる原子位置で記述される。
六角形ユニットセルとは
六方晶系結晶の単位胞のこと。
六角形の結晶構造を持つ物質の原子の配置を表している。
同じ長さの2本の軸と、異なる長さの1本の軸を持つ。
この軸は、他の2つの軸に対して垂直です。
2つの軸の間の角度は120oです。
六角形ユニットセルの具体的な特徴は、次の通りです。
- a=b≠c
- α= β=90o
- γ=120oです。
単斜晶系単位胞とは？
単斜晶系の単位胞のことで、単斜晶構造を持つ物質の原子の配列を表す。
単斜晶系を持つ物質の原子の配置を表している。
単位胞の3軸（a、b、c）は不等間隔です。
単斜晶系の単位は平行四辺形を底辺とする直方体です。
平行四辺形は、2組の平行な辺を持つ単純な構造です。
したがって、2つの軸は互いに90oの角度で交わる。
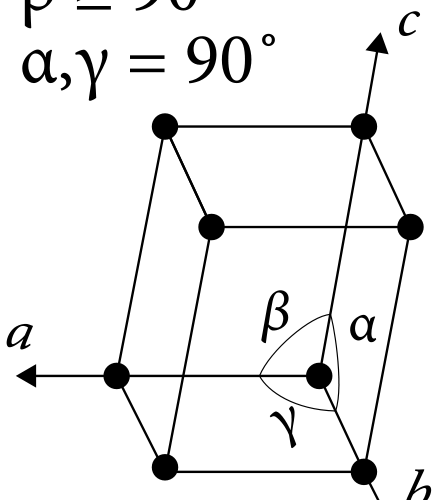: 図3: 単斜晶系ユニットセル
六角形ユニットセルの具体的な特徴を簡単に説明します。
- a≠b≠c
- α= γ =90o
- β≠90o
六角形と単斜体の単位格子の違い
定義
六方晶系単位胞: 六方晶系の単位胞。
単斜晶系単位: 単斜晶系結晶の単位胞。
軸の長さ
六角形ユニットセル: 六角形ユニットセルは、同じ長さの2つの軸と異なる長さの1つの軸を持つ(a=b≠c)。
単斜晶系ユニットセル: 3本の軸の長さが不揃い(a≠b≠c)のもの。
角度
六角形ユニットセル: 六角形ユニットセルは、αとβの角度が90°に等しく、γは120°に等しい。
単斜晶系ユニットセル: 単斜晶系ユニットセルは、αとγの角度が90°に等しく、βは90°に等しくない。
平行四辺形の有無
六角形ユニットセル：六角形ユニットセルは、ユニットセル内に平行四辺形構造を持たない。
単斜晶系単位胞: 単斜晶系単位胞は単位胞の底に平行四辺形構造を持つ。
結論
六角形と単斜晶の単位胞は、結晶系の原子配列の繰り返しパターンを表す部分です。
六角形単位胞と単斜晶単位胞の主な違いは、六角形単位胞が同じ長さの2つの軸を持つのに対し、単斜晶単位胞は長さが不揃いの3つの軸を持っていることである。
