定立と定理の主な違いは、定立が何の証明もなしに真であると仮定されるのに対し、定理は真であることを証明することができ、また証明しなければならない点です。
定理と仮定は、幾何学で見られる2つの概念です。
実は、これらは幾何学的な真理を述べたものです。
ポスチュレートとは、証明の必要がないほど明らかに正しいと考えられる考え方のことです。
定理は、真であることを証明できる/しなければならない数学的な記述です。
ポスチュレートとは
ポスチュレートとは，私たちが何の証明もなしに真であると仮定する数学的な記述です．これは，証明の必要がないほど明らかに正しいと考えている考え方です．例えば，直線は少なくとも2つの点を含むというのは，定立方程式です．これは非常に明白であり、一般に受け入れられているので、私たちは通常、これを真と認めるのに何の証明も必要としない。
私たちは定理やレンマを定理をもとに作ります。
実際、1つ以上のポスチュレートから定理を作ることは可能である。
図1：ユークリッドの平行ポスチュレート
ポスチュートの基本的な特徴
- 例えば、理解しにくい言葉をたくさん使ってはならない。
- 他の定石と組み合わせたときに一貫性があること。
- 単独で使えるものでなければならない。
しかし、ある仮定が常に正しいとは限らないということも知っておく必要がある。
新しい発見があると、定説が正しくないことが判明することがあります。
例えば、アインシュタインの「宇宙は均質である」という仮定は、もはや正しいとは認められていない。
定理とは
定理とは、私たちが真であると証明できる数学的な記述です。
論理的な推論や、既に証明されている他の定理を使って証明することができます。
実際、他の定理を証明するために証明しなければならない定理をレンマと呼びます。
ポスチュレートは、レンマと定理の両方を構築するための基礎となるものです。
四色定理、ピタゴラスの定理、フェルマーの最終定理などは定理の一例です。
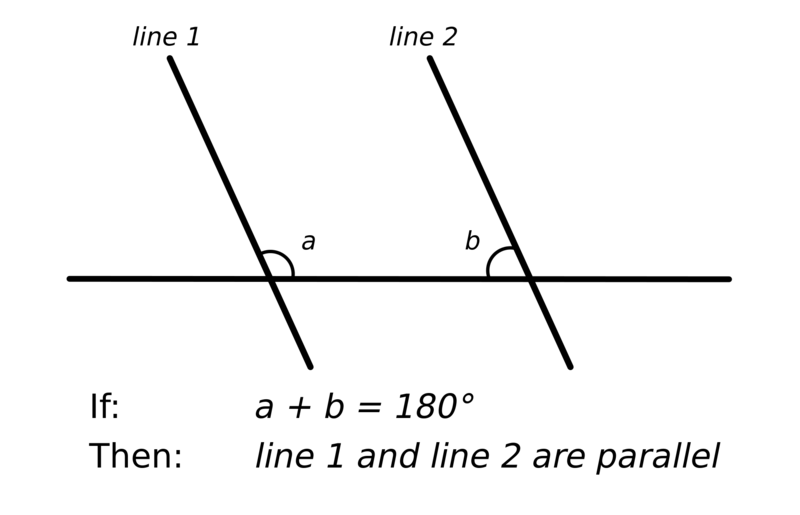図02: ピタゴラスの定理
ピタゴラスの定理
ピタゴラスの定理によると、直角（90°）の三角形の3辺がそれぞれ正方形を構成しているとき、最大の正方形は他の2つの正方形を合わせたものと同じ面積を持つ。
つまり、直角三角形の斜辺の2乗は、他の2辺の2乗の和に等しいのです。
このことは、a2 + b2 = c2 という方程式を使って示すことができる。
ポスチュレートと定理の関係
- 定理と定立は、幾何学的な真理を記述したものです。
- 定理は定立をもとに作られます。
推論と定理の違い
定義
定石とは、私たちが何の証明もなしに真であると仮定する数学的記述であり、定理とは、私たちが真であることを証明できる、または証明しなければならない数学的記述です。
証明
仮定は証明なしで真とされるが、定理は真であることを証明できる。
証明の必要性
さらに、定立は自明なことを述べているので証明する必要はないが、定理はそれほど自明ではないので、論理的な推論やレンマを用いることで証明することができる。
結論
定立方程式は、私たちが何の証明もなしに真であると仮定する数学的記述であり、定理は私たちが真であることを証明できる、または証明しなければならない数学的記述です。
したがって、定立と定理の主な違いは、その証明にある。
