高校数学、特に『数列』の公式は種類が色々あるし、aとかnとか文字がやたらと書かれていて意味が分からない、と言う人が多い気がします。
そこで今回は、数列の中でも最も基本的な『等差数列の和』の公式に絞って、その理論とか証明を超分かりやすく説明していきます!
ボクも高校生の時は「数列なんて公式暗記&計算ゲーだろ?」と思っていたのですが、この等差数列の和の理論を知って数学にハマりそうになってます。
ぜひ、今後の学習の参考にして下さい。
等差数列の和の公式は小学生並みの理論でできている
等差数列の和の公式と言えば下の式が超有名ですが、考えてみれば、なぜこんな式が「1,3,5,7・・・」と言う数の集まりの和になるのかが不思議に感じませんか?
だって、「最初と最後の数(初項と末項)を足して、後は項数の半分をかけたら、はい数列の和」って、何してんの?って感じですよね。
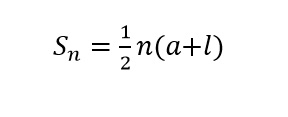
しかし、この一見理解ができなさそうな「等差数列の和の公式」ですが、驚くことに「小学3年生でも理解できるぐらい簡単な理論で成り立っている」のです。
等差数列の和の公式の理論
例えば、下図の様な数列があるとしましょう。
下の数列は、初項が1で公差が2の、教科書の例題にも出てきそうなぐらい簡単な数列です。
で、この数列の和を求めていきたいわけです。

まあ、この程度の簡単な数列であれば、「暗算」と言う名の気合いで何とかなるかもしれませんが、以下の方法でもっと楽に、そして確実に和を求めることができます。
数列の和の計算を楽にする方法
その方法とは、まずは数列の初項と末項、つまり数列の端っこ同士を足し算していきます。
端っこの数は「1」と「11」なので、足して「12」になりますね。
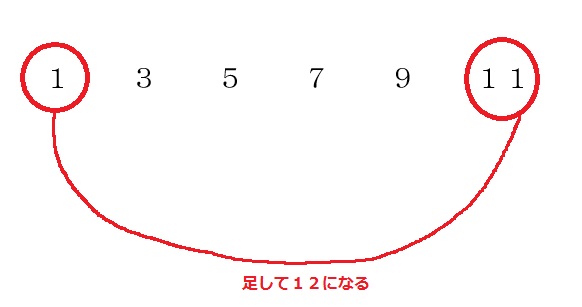
ちなみに、この端っこ同士を足す作業は、公式で言う所の「a+l」の部分に該当します。
そして同様に、端っこから2番目同士の数を足していき、さらに端っこから3番目同士の数を足していきましょう。
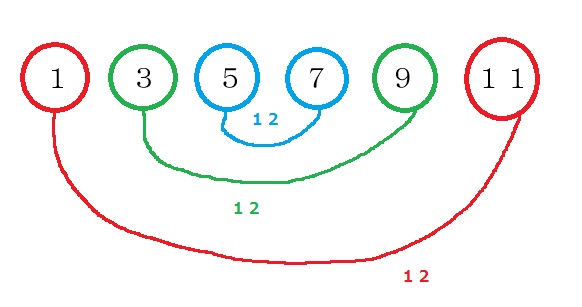
このように「端っこ同士、端っこから2番目同士・・・」と言う風に数を足していくと、全てのペアが「12」になります。
つまり、公式風に言うと、全てのペアが「a+l」になる、と言うわけです。
じゃあ、この12(a+l)のペアがいくつできたかを数えていきましょう。
先ほどの数列の項数は、「1,3,5,7,9,11」の全部で6つありました。
そして、その6つの数を使って2つで1組のペアを作ったので、ペアは全部で「6×1/2=3ペア」と言うことになります。
よって、12のペアが3つあるので、答えは36になります。
ちょっと、ここで注目してほしいのは「6×1/2」と言う計算。
これは、今回の数列の項数が6だからこの式になっているわけですが、もし、項数がnだったら、この計算式は「n×1/2」になるわけです。
つまり、12(a+l)のペアがn×1/2つできたわけだから、答えは1/2n(a+l)になる!これこそ、まさに「等差数列の和の公式」ではありませんか!
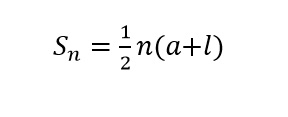
このように、実は等差数列の和の公式って、めちゃめちゃ簡単な理論によって作られていることが分かったと思います。
等差数列の和の公式ももう片方の式の証明
等差数列の和の公式には、上記で説明した形の他に、以下のようなものがありました。
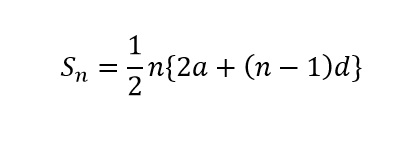
一見複雑に見えますが、先ほどの公式の意味が分かれば、コイツも一発で理解できます。
まずは、この式の中カッコの中身を見て下さい。
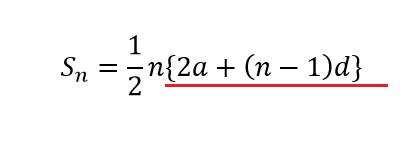
で、この中の2aと言う文字を「a+a」と分けてあげます。

つまり、等差数列の和の2種類の公式って、全く同じ意味を持っている式だったんですね。
等差数列の和の公式を厳密に証明していく
上記までの証明方法は、あくまでも「等差数列の和の公式って、小学生でも理解できるんやでー」と言うのを知るための証明で、公式を覚えるのに適した形になります。
しかし、テストとかで「公式を証明せよ」と言う問題が出されたら、以下の証明方法を使う必要があります。
厳密な等差数列の和の証明方法
と言っても、厳密な証明の方も、理論的な部分は結構簡単です。
まずは、等差数列の一般項の公式を思い出してみましょう。
等差数列の一般項は、以下の様な式でした。
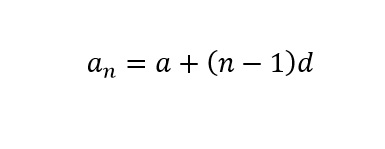
なので、初項から第n項まである数式の場合は、上の公式に当てはめていくと、初項(n=1)は「a」、第2項(n=2)は「a+d」と表せますし、末項(n=n)は、「a+(n-1)d」と表せます。
そして、この等比数列の初項から末項までの式を、全部ダーッと足していきます。
すると、下のような等差数列の和の式ができあがります。

でも1つでは物足りないので、もう1つ上と同じ式を書き加えましょう。
ただし、上の式は初項から順番に書いていきましたが、今度は末項から逆の順番に書いていきましょう。

このように、ただ数式の順番を入れ替えただけの等差数列の和の式を2つ用意しました。
そして、今度はこの2つの式を足します。
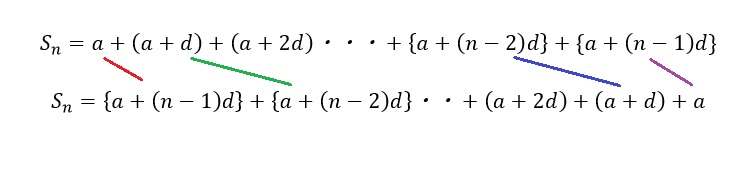
足し算をしていくと、左辺は2Sとなります。
そして右辺は、「左から1番目同士を足して、左から2番目同士を足して・・・左からn番目同士を足す」と言う風に足し算をしていきます。
すると、右辺では{2a+(n-1)d}と言う式がn個できあがるので、右辺は「n{2a+(n-1)d}」と書き表せます。
ここまで来ると、もう等差数列の和の公式が見えてくるでしょう。
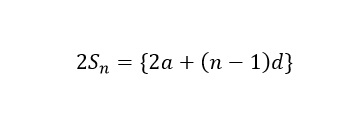
後は両辺を2で割るだけで、等差数列の和の公式の完成です。