ツリーとグラフの主な違いは、ツリーが木構造の階層構造でデータを整理するのに対して、グラフはネットワークとしてデータを整理することです。
データ構造とは、データを体系的に整理する方法です。
データ構造には、主に線形データ構造と非線形データ構造の2種類があります。
そして、一般的な非線形データ構造として、ツリーとグラフがあります。
ツリーとは
ツリーとは、データを木に見立てて並べたデータ構造のことです。
ノードは、ツリー内のデータ項目です。
主要なノードはルートであり、他のノードはその子ノードです。
これらのノードはすべて空でない集合に配置され、それぞれがサブツリーとなる。
さらに、ノード間には親子関係が存在する。
1つの親ノードは複数の子ノードを持つことができ、各子ノードに対して親ノードは1つしか存在できない。
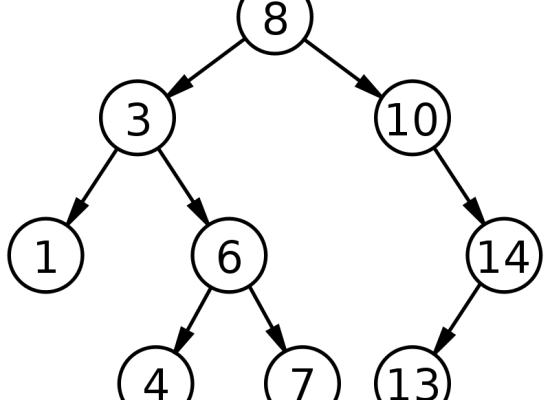
木に関する重要な用語は次のとおりです。
上記のツリーでは、これらの特徴や例を見ることができる。
ルートノードとは、ツリー内の最上位のデータ項目です。
上の画像では、要素8がルートノードです。
エッジは、ノード間の接続に役立つ。
例えば、上のツリーでは、8と3、8と10がエッジで結ばれている。
親ノードとは、ルートノード以外のノードで、エッジによって上方に接続されるノードのことである。
例えば、3は1と6の親ノードです。
同様に、6 は 4 と 7 の親ノードです。
子ノードとは、エッジによって下方向に接続されるノードです。
たとえば、4 と 7 は 6 の子ノードです。
葉ノードとは、子ノードを持たないノードのことである。
上の木では、1, 4, 7, 13 がリーフノードです。
サブツリーは、ノードの子孫です。
例えば、ルートノード(8)の左側で、3から始まる部分がサブツリーです。
同様に、ルートノード(10)から始まる右側のセクションはサブツリーです。
レベルは、ノードの世代を表す。
例として、ルートノードはレベル0に属する。
3と10はレベル1に属し、以下同様です。
さらに、木には大きく分けて2分木と2分探索木があります。
2分木では、各ノードは最大2個の子ノードを持つことができる。
二分探索木は、順序付き二分木です。
グラフとは
グラフとは、オブジェクトの集合を絵で表現したデータ構造で、いくつかのオブジェクトのペアをリンクでつないだものです。
通常、グラフはネットワークを表現するのに役立つ。
グラフに関連する重要な用語は以下の通りです。
頂点はオブジェクトまたはデータ項目です。
円はそれらを表す。
上のグラフでは、A,B,C,Dが頂点です。
頂点はV = {A,B,C,D}と書くこともできる。
エッジは、頂点と頂点を結ぶリンクです。
例えば、上のエッジは、AとBの頂点、BとDの頂点などを結んでいます。
エッジはE = {AB, BC, BD, DC}と書くこともできる。
経路は、目的地のノードに到達するためにたどるべきノードの順序を表す。
例えば、ABDは頂点AからDへの経路を表す。
2つのノードがエッジでつながっているとき、そのノードは隣接ノードとなる。
例えば、AとBは隣接ノードです。
同様に、BとDは隣接ノードです。
グラフに対して行える主な操作は、頂点の追加、辺の追加、頂点の表示です。
グラフには主に有向グラフと無向グラフの2種類があります。
グラフが順序のある頂点の組を含むとき有向グラフとなり、順序のない頂点の組を含むとき無向グラフとなります。
ツリーとグラフの違い
定義
木はルートと親ノードを持つ子ノードのサブツリーからなる階層的な木構造を模したデータ構造であるのに対し、グラフはエッジで結ばれた頂点の集まりからなるデータ構造です。
したがって、これがツリーとグラフの根本的な違いです。
タイプ
また、木は大きく分けて2分木と2分探索木があります。
一方、グラフは大きく分けて有向グラフと無向グラフの2種類があります。
データ表現
木はデータを木構造で階層的に表現し、グラフはデータをネットワークに近い形で表現する。
したがって、これがツリーとグラフの大きな違いです。
ルートノード
さらに、木とグラフのもう一つの大きな違いは、木にはルートノードがあるのに対して、グラフにはルートノードがないことである。
ループ
さらに、ループの有無も木とグラフの違いのひとつです。
木にはループがないが、グラフにはループがある場合があります。
複雑さ
さらに、グラフは木よりも複雑です。
結論
木とグラフは2つの非線形データ構造です。
木とグラフの主な違いは、木が木構造の階層構造でデータを整理するのに対し、グラフはネットワークとしてデータを整理する点です。
