天然に存在する同位体の中には、原子核に含まれる陽子と中性子の数が不均衡なために不安定なものがあります。

そのため、これらの同位体は安定になるために、放射性崩壊と呼ばれる自発的な過程を経ます。

放射性崩壊により、ある特定の元素の同位体が別の元素の同位体に変換されます。

しかし、放射性崩壊の最終生成物は、常に最初の同位体よりも安定です。

ある物質の放射性崩壊は、半減期と呼ばれる特別な用語で測定されます。

 ある物質が放射性崩壊によって最初の質量の半分になるまでの時間を、その物質の半減期として測定します。

これが、放射性崩壊と半減期の関係です。

放射性廃棄物とは

放射性崩壊とは、不安定な同位体が放射線を出して崩壊していく過程をいいます。

不安定な同位体とは、不安定な原子核を持つ原子のことです。

原子は、原子核に多数の陽子が存在する、あるいは原子核に多数の中性子が存在するなど、いくつかの理由で不安定になることがあります。

これらの原子核は、安定になるために放射性崩壊を起こします。

陽子が多すぎたり、中性子が多すぎたりすると、原子は重くなります。

この重い原子は不安定です。

したがって、これらの原子は放射性崩壊を起こすことができます。

他の原子も、中性子と陽子の比率によって放射性崩壊を起こすことができます。

この比率が高すぎると、中性子が豊富で不安定になります。

この比率が低すぎると、陽子を多く含む原子となり、不安定になります。

物質の放射性崩壊は、主に3つの方法で起こる可能性がある。

• アルファ線放出/崩壊
• ベータ線放出/崩壊
• ガンマ線放出/崩壊

α線放出

アルファ粒子は、ヘリウム原子と同じものです。

陽子2個と中性子2個で構成されている。

アルファ粒子は、2個の陽子の正電荷を中和する電子がないため、+2個の電荷を帯びている。

アルファ崩壊により、同位体は陽子2個と中性子2個を失う。

したがって、放射性同位元素の原子番号は2単位、原子質量は4単位減少する。

ウランのような重元素はアルファ崩壊を起こすことができます。

ベータ線放出

ベータ線放出(β)の過程では、ベータ線粒子が放出されます。

このとき、β粒子の電荷によって、正電荷のβ粒子と負電荷のβ粒子とがあります。

β-放出であれば、放出される粒子は電子です。

β＋放出であれば、その粒子は陽電子です。

  陽電子とは、電荷を除けば電子と同じ性質を持つ粒子です。

電子の電荷が負であるのに対し、陽電子の電荷は正です。

ベータ線放出では、中性子が陽子と電子（または陽電子）に変換される。

したがって、原子質量は変化しないが、原子番号が1単位増えることになる。

ガンマ線放出

ガンマ線は粒子状ではありません。

したがって、ガンマ線は原子の原子番号や原子質量を変えることはありません。

ガンマ線は光子で構成されています。

この光子はエネルギーだけを運びます。

したがって、ガンマ線は同位体にエネルギーを放出させるのです。

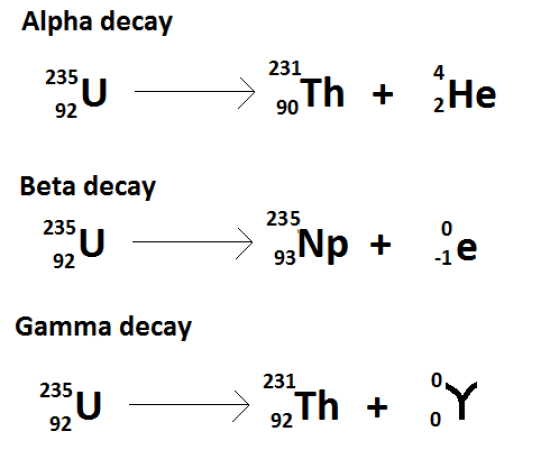図1: ウラン235の放射性壊変

ウラン235は天然に存在する放射性元素です。

この元素は、異なる条件下で3種類の放射性崩壊を起こすことができます。

半減期とは

ある物質の半減期とは、その物質が放射性壊変によって最初の質量または濃度の半分になるまでにかかる時間のことである。

この用語は、t1/2という記号で表される。

個々の原子がいつ崩壊するかは予測できないので、半減期という言葉が使われる。

しかし、放射性元素の原子核が半分になるまでの時間を測定することは可能である。

半減期は、原子核の数か濃度のどちらかで測定することができます。

同位体によって半減期は異なる。

そのため、半減期を測定することで、特定の同位体の有無を予測することができます。

半減期は、物質の物理的状態、温度、圧力、その他の外部からの影響に依存しません。

物質の半減期は次の式で求めることができる。

ln(Nt / No) = kt

ここで

Nt は t 時間後の物質の質量

No は物質の初期質量

K は崩壊定数

tは考慮した時間

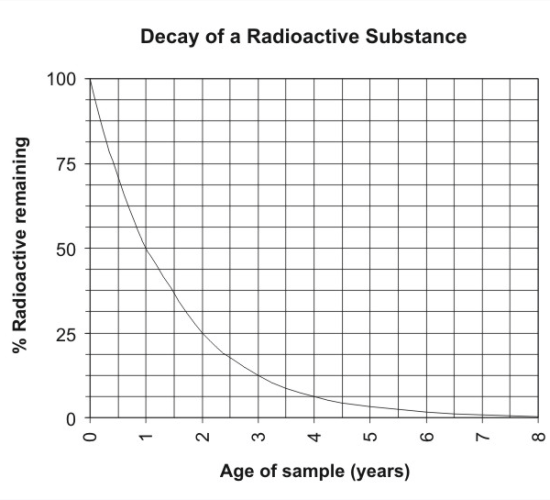図02: 放射性崩壊の曲線
放射性物質の壊変曲線

上の図は、ある物質の放射性壊変の曲線を示している。

時間の単位は年です。

このグラフによると、初期質量（100%）から50%になるまでの時間は1年です。

100%が2年後に25%(初期質量の4分の1)になる。

したがって、その物質の半減期は1年です。

100% → 50% → 25% → 12.5% → → →

(第1半減期) (第2半減期) (第3半減期)

上記のグラフは、グラフから得られた内容を要約したものです。

放射性崩壊と半減期の関係

放射性物質の壊変と半減期には直接的な関係があります。

放射性崩壊の速度は半減期換算で測定される。

上記の式から、放射性物質の壊変速度を計算するためのもう一つの重要な式を導き出すことができる。

ln(Nt / No) = kt

となり、半減期を過ぎると質量（または原子核の数）は初期値の半分になることから

Nt = No/2

とすれば

ln({No/2}/ No) = kt1/2

ln({1/2}/ 1) = kt1/2

ln(2) = kt1/2

したがって

t1/2 = ln2 / k

ln2 の値は 0.693 です。

t1/2 = 0.693 / k となります。

ここで、t1/2 は物質の半減期、k は放射性崩壊定数です。

以上の式から、放射性の高い物質は早く消費され、放射性の弱い物質は完全に崩壊するまでに長い時間がかかることがわかります。

したがって、半減期が長いと放射性物質の崩壊が速く、半減期が短いと放射性物質の日数が遅いことを示している。

物質によっては、放射性崩壊に数百万年かかるものもあるので、半減期を決めることはできない。

結論

放射性崩壊は、不安定な同位体が放射線を出して崩壊する過程です。

放射性崩壊の速度は半減期の等価値で測定されるため、物質の放射性崩壊と半減期には直接的な関係があります。